

Threaded Binary Tree
Get started
জয় শ্রী রাম
🕉Threaded Binary Trees are the binary trees where we utilize either the left child pointer or the right child pointer or both of the leaf nodes to achieve something meaningful or optimizing some kind of tree traversal. In the next few chapters we will see how Threaded Binary Tree concept will improve the space complexity of Morris Preorder Traversal, Morris Inorder Traversal and Morris Postorder Traversal from O(n) to O(1).
Types of Threaded Binary Tree:
Threaded Binary Tree can be of two types:
-
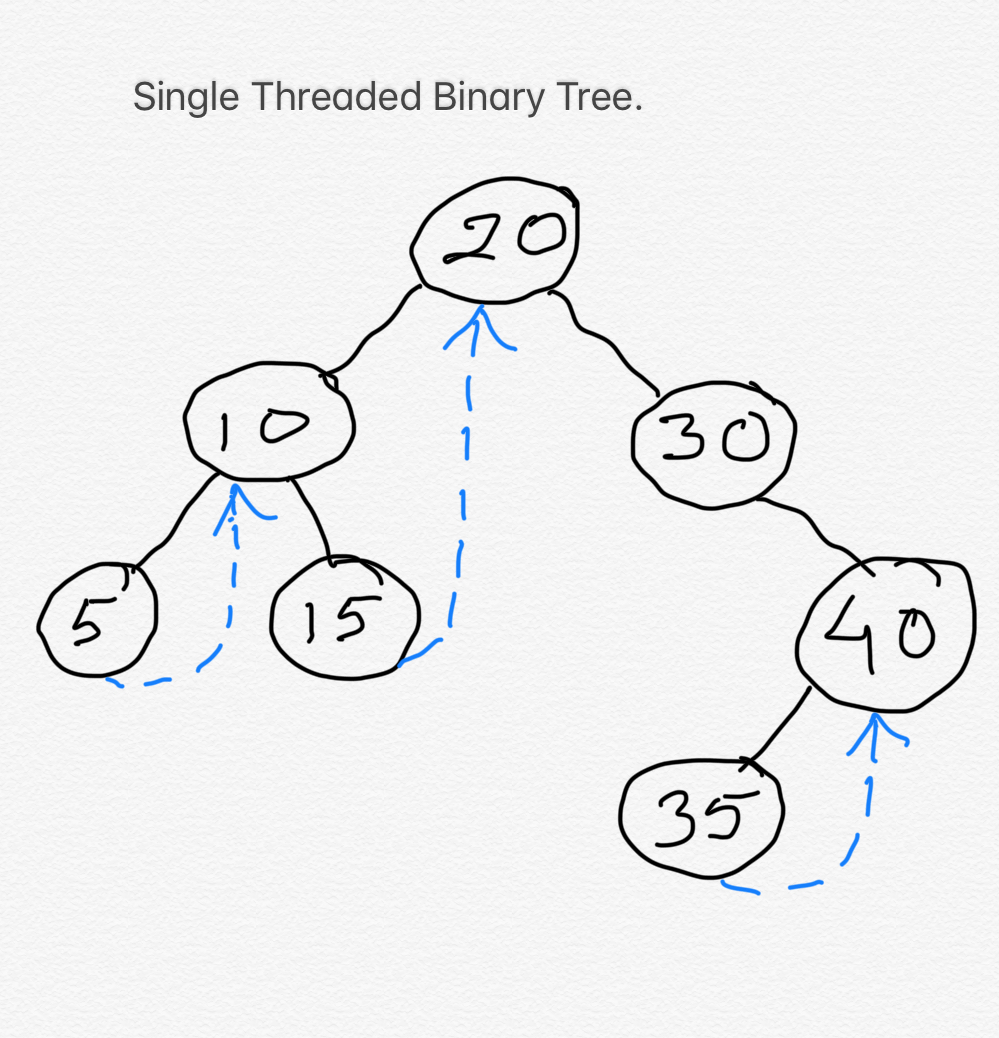
Single Threaded Binary Tree: In Single Threaded Binary Tree we use either the left
child node pointer or right child node pointer of the leaf nodes to add any information.
In the below diagram the special threaded links are shown by dashed arrows. In this diagram right child pointer of each leaf node is pointing to the inorder successor node for that leaf node.
-
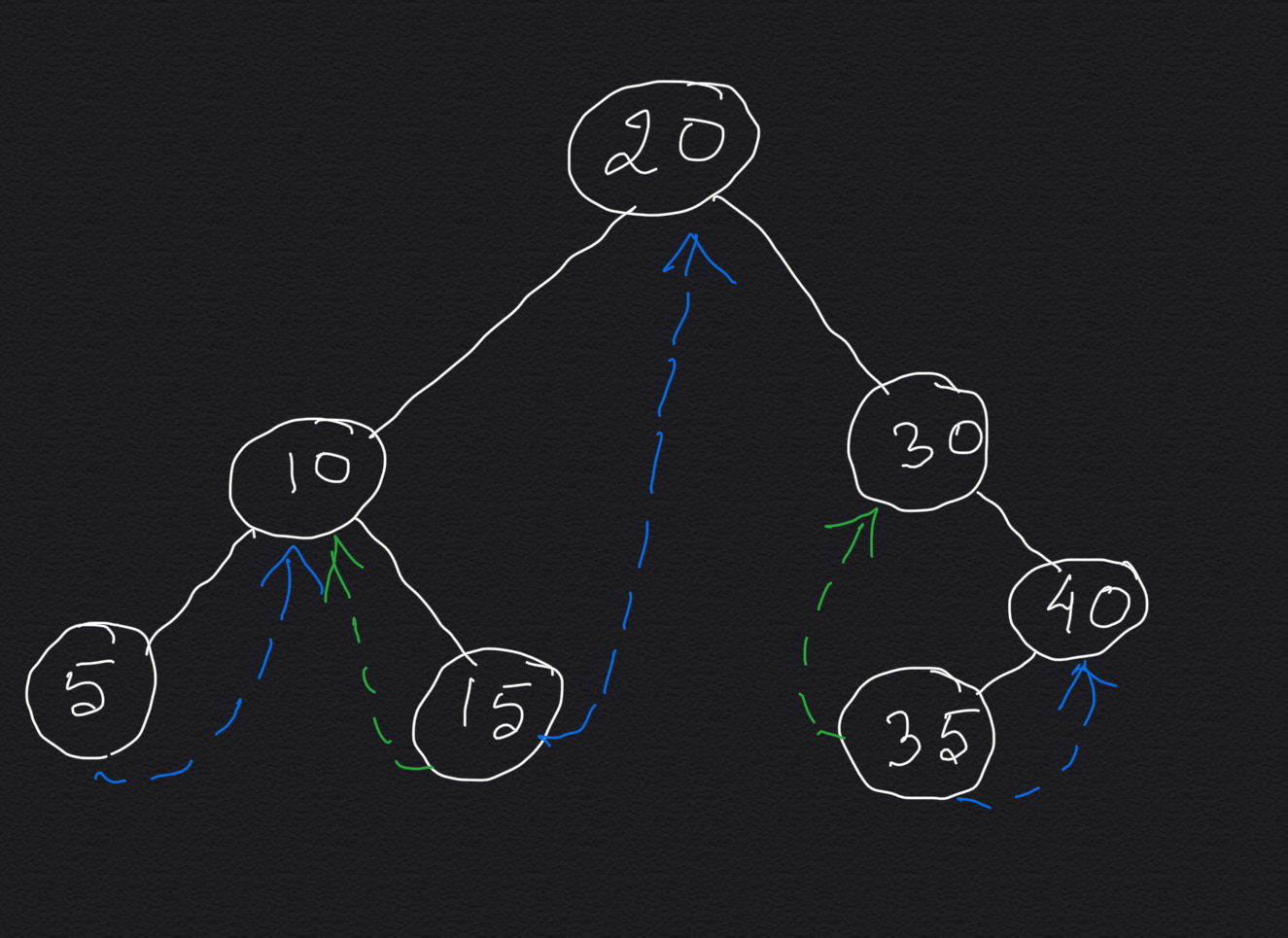
Double Threaded Binary Tree:In Double Threaded Binary Tree
we use both the left
child node pointer and right child node pointer
of the leaf nodes to store any additional information.
In the below diagram the special threaded links are shown by dashed arrows. In this diagram left child pointer of each leaf node is pointing to the inorder predecessor node for that leaf node and the right child pointer is pointing to the inorder successor node for that leaf node.
An entire binary tree can be easily traversed when you have access to the root, but given only a pointer to a node, finding the node which comes next may be slow or impossible. For example, leaf nodes by definition have no descendants (or, successors), so no other node can be reached given only a pointer to a leaf node. A threaded tree adds extra information in some or all nodes, so the "next" node (successor node) can be found quickly. It can also be traversed without recursion and the extra storage (proportional to the tree's depth in average case and proportional to total number of nodes in worst case when the tree is skewed or chained) that requires.
A Threaded Binary Tree is defined as follows:
" A binary tree is threaded by making all right child pointers that would normally be null point to the in-order successor of the node (if it exists), and all left child pointers that would normally be null point to the in-order predecessor of the node. "
Threaded Binary tree solves two major problems:
- Iterative (without using threaded binary tree concept) and recursive implementation of tree traversal use stack space proportional to the height of a tree. If the tree is fairly balanced, this amounts to O(log n) space for a tree containing n elements. In the worst case, when the tree takes the form of a chain, the height of the tree is n so the algorithm takes O(n) space.
- A second problem is that all traversals must begin at the root when nodes have pointers only to their children. It is common to have a pointer to a particular node, but that is not sufficient to get back to the rest of the tree unless extra information is added, such as thread pointers.
To better understand the applications of Theaded Binary Tree please read the next three chapters of this series, as mentioned below:
